記得以前中學物理課的時候,老師曾經出過一道問題,設層層疊積木的長為a,那麼在桌子邊把兩塊積木疊起來,最多可以令它們伸出桌邊多長的距離而不倒塌呢?這個問題其實不難,但史丹福卻被這問題吸引了,自己繼續思考,如果把10塊層層疊積木疊起來,又最多可以伸到多長呢?如果有無限多塊層層疊積木,又最多可以伸到多長?今次我們特意請來奶油貓Peaches為我們作出示範,解釋這條問題。
首先,如果層層疊積木的密度平均的話,重心一定在最中間的一點。要令到積木不倒塌,重心就一定要被承托著。
放第一塊層層疊積木時,只要把它的重心放在桌邊,那麼它的重心被桌子承托著,便不會倒塌,所以伸出的長度是a/2。
當有兩塊層層疊積木時,第二塊積木的重心必須又第一塊積木承托著。把第二塊積木的重心放在第一塊積木的最右端,這時兩塊積木合共的重心(下圖中的紅色交叉)位於兩塊積木中間,把共同重心放在桌子邊上,層層疊積木伸出了多a/4,共伸出了3a/4。
但如果再加多幾塊積木,情況就開始複雜了。我們已經不能再在上面加積木,第三塊積木只要比第二塊伸出一點,三塊積木合共的重心就會伸到桌邊之外而倒下。但我們可以在下面放,把第三塊積木的最右端放在首兩塊積木的合共重心之下,然後把三塊積木的合共重心放在桌邊,這樣就可以把三塊積木放到最出。留意,積木伸出的長度其實是最高一塊積木最右端與三塊積木合共重心的水平距離。
我們繼續用類似的方法去放第四塊、第五塊、...、第n塊積木,也就是把第n塊積木的最右端放在之前n-1塊積木的合共重心之下,再把全部n塊積木的合共重心放在桌子邊,這樣就可以伸到最出而不倒塌。
回到文中最初的問題,要知道10塊層層疊積木疊起來伸到多長,只要代入我們剛得出的公式就可以了,大家可以自行試試。
另外,如果我們有無限多塊層層疊積木,理論上是可以伸到無限遠的,並沒有上限。 1+1/2+1/3+1/4+...是一個很有名的,直覺上看起來好像會收斂(converge),但其實是發散(diverge)的級數。因為
無限個1/2加起來是發散(diverge)的,1+1/2+1/3+1/4+...也自然是發散的。





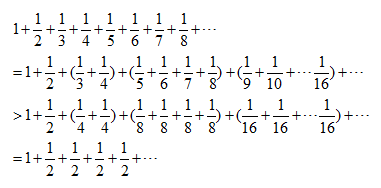
沒有留言:
張貼留言