聖誕襪定理

這是篇遲來的聖誕文章。雖然聖誕已過，但我們不妨再探討多一個與聖誕有關的數學定理──聖誕襪定理（Christmas stocking theorem）。聖誕襪定理與組合數學中的柏斯卡三角有關，是一條簡單但有趣的初等數學定理。

相信大家都見過大名鼎鼎的帕斯卡三角（Pascal triangle），它是由二項式系數所組成的，第n+1行的數字是_nC₀至_nCn。

帕斯卡三角有很多有趣的性質，我們就在此簡單地列舉幾個。

性質一：帕斯卡三角形中相鄰的兩個數字相加等如底下的數字

因為

這大概是帕斯卡三角形最重要的性質，事實上也有人用這個性質去定義帕斯卡三角形。

性質二：帕斯卡三角形中第n行的數字相加等如2^n-1

這可以用二項式定理（binomial theorem）來解釋：

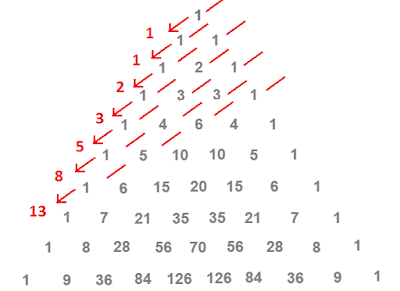
性質三：帕斯卡三角形的數字如下圖般沿左下相加，會得到斐波那契數列（Fibonacci sequence）

也就是說，

其中F_n是指斐波那契數列中的第n個數。

我們可以用數學歸納法來證明：

性質四：帕斯卡三角形中第n+1行數字的平方相加，就等如第2n+1行最中間的數字

也就是說

因為

重溫了這些有趣的性質後，我們終於入正題了，把帕斯卡三角形中的數字如下圖般沿右下相加，答案就是最右下數字下面的數字。

也就是說：

觀看上圖中數列的形象，就如一對聖誕襪，因此數學家就形象化地稱它為「聖誕襪定理」，也有人稱它為「曲棍球棒定理」（hockey stick theorem）。 我們當然可以用「屈機」的數學歸納法去證明這公式，不過史丹福打算用一個較有趣及直觀的方法去解釋。以下圖中的70為例，根據性質一，

70 = 35 + 35 = (15 + 20) + 35 = [(5 + 10) + 20] + 35 = { [(1 + 4) + 10] + 20} + 35 = 1 + 4 + 10 + 20 + 35。

根據這個概念，我們只要重覆使用帕斯卡三角形的性質一，就會得出這條很有聖誕氣氛的聖誕襪定理。

雖然聖誕已過，史丹福還是想藉此機會在2019年的最後一天祝大家新一年事事順心，知識積水成淵。

聖誕特輯：聖誕樹般的骨髓

史丹福與Peaches先在此祝大家聖誕快樂。相信對很多人來說，上年都是令人心傷的一年，希望下年會更好，香港人終會獲勝。

史丹福每年聖誕都會介紹一個與節日相關的題目，今年我就特意選擇了一張很漂亮的骨髓環鑽活檢（trephine biopsy）染片，就像聖誕樹般在黑暗中閃閃發亮，很具聖誕氣氛。這個骨髓環鑽活檢樣本來自一位50多歲的男士，他因泡沬尿入院，之後驗出有嚴重的蛋白尿。大家猜猜他患有甚麼病，骨髓又為何閃閃發亮。

如聖誕樹般在黑暗中閃閃發亮骨髓抹片

如聖誕樹般在黑暗中閃閃發亮骨髓抹片

聖誕樹

原來病人患有類澱粉沉積症（amyloidosis）。顧名思義，澱粉蛋白沉積症就是類澱粉積聚而引起。類澱粉蛋白（amyloid protein）是一種有毒的蛋白，它可以積聚在心臟、腎臟、神經等不同的器官或組織，做成破壞。

類澱粉蛋白明明就是蛋白質，為何我們又稱它為「類澱粉」呢？這名字不是很尷尬嗎？原來早期的碘染色技術尚未成熟，令科學家錯誤地以為類澱粉蛋白是一種澱粉。當時科學界其實一直在爭論它到底是脂肪沉澱物，或是碳水化合物沈澱物，直到最後卻爆出個大冷門，發現它其實是一種蛋白質。在分子結構來說，類澱粉蛋白分子中有約95%是原纖維（fibril）結構，另外5%屬於P成分（P component）。

類澱粉蛋白沉積症可分為局部性及全身性，如惡名昭彰的俗稱「老人痴呆症」的阿茲海默症（Alzheimer's disease）就是由於Aβ類澱粉蛋白局部性地積聚在大腦中，令大腦細胞壞死而引起的。

不過要數破壞力最多，最致命的類澱粉沉積症，始終是全身性的類澱粉沉積症。它可以積聚在心臟引起心臟衰竭，積聚在腎臟中引起腎病，積聚在神經中引起神經病變，它們甚至可以影響凝血因子，造成出血症狀。

在眾多的全身性類澱粉沉積症中，以AL類澱粉沉積症是最為常見。AL類澱粉沉積症其實是一種血液科的疾病。大家都記得，漿細胞是一種負責製造抗體的細胞吧？它是一種重要的免疫細胞，不過惡性的漿細胞過度增生而引起的血液癌症，例如多發性骨髓瘤（multiple myeloma）。然而，惡性的漿細胞還可以製造大量的免疫球蛋白輕鏈，這些免疫球蛋白輕鏈可以組合成有害的AL類澱粉蛋白，毒害不同器官。我們在文中最初提到的病人，就是因為AL類澱粉蛋白積聚了在腎臟，破壞了腎小球，令到血液中的蛋白質可以經過腎臟不斷排出，因而形成蛋白尿。

要診斷類澱粉沉積症，我們只需把組織樣本用剛果紅（Congo red）染料作上色，然後用利用偏振光在顯微鏡下觀察，就會見到它呈現蘋果綠色。

大家在中學物理課中都學習過偏振光（polarized light）吧？簡單來說就是電場的振盪只朝著單獨一個方向的光。這個有有趣的物理學現象原來也是醫學診斷中的重要工具啊！

例如在文中最初的環鑽活檢染片中，病人的骨髓中的類澱粉蛋白吸收了剛果紅染料，所以在未加偏振濾鏡時呈現如聖誕老人衣服般的紅色。但當加了偏振濾鏡之後的影像，大家可以見到蘋果綠色的光，如聖誕燈飾般發亮，那些就是類澱粉蛋白了。根據史丹福的經驗，骨髓中的是類澱粉蛋白一般都只會呈現弱弱的蘋果綠色線，如這圖般壯觀的景象，非常少見。

為什麼類澱粉蛋白會有這樣特別的特性呢？簡單的解釋是類澱粉蛋白有特別的化學結構，它與剛果紅染料結合後會出現雙折射（birefringence）的光學特性，它的折射率取決於進入的光的偏振方向。如果把正常的物料（如玻璃）放在兩個互相垂直的偏振濾鏡之間，應該完全沒有光可穿過。但雙折射的物料可以把偏振方向改變，所以把這些物料放在兩個互相垂直的偏振濾鏡之間，就有特別顏色的光可以通過了。

至於治療方面，AL類澱粉沉積症的患者一般都會接受類似多發性骨髓瘤的化療藥物組合，年輕的患者亦可考慮接受自身骨髓移植。但由於AL類澱粉蛋白常積聚於心臟中，所以很多病人的心臟功能都差得過分，以至不能承受自身骨髓移植。

雖然類澱粉蛋白在剛果紅染料與偏振光下會製造出如聖誕燈飾般漂亮的光芒，但諷刺地類澱粉沉積症卻是一個很致命的疾病。但願在這個普天同慶的節日中，病人們可以盡快康復，免於疾病之苦。

Peaches與聖誕Pepe再在此祝大家聖誕快樂。

小明行樓梯2

史丹福回家時要行上很長的樓梯，途中經常會思考到有趣的數學問題。之前史丹福就討論過一條「小明上樓梯」的問題。今次我們再轉換一下情景。

假如小明要行上一道100級的樓梯，假如這次小明的腿變短了，他可以每次最少行上1級，最多只可以一次上2級。問他有多少種方法去行上這道100級的樓梯？

沒有頭緒？當做數學題做到毫無頭緒的時候，我們不妨試試由較簡單的問題入手，再找找規律。

設小明只可以每步只可以上一級或兩級樓梯，他共要上n級樓梯，總共有s_n個方法。我們的問題要求的是s₁₀₀。

如果他需上零級樓梯，那麼他當然只有一個方法，就是企定定一級都不上，所以s₀ = 1。如果他需上一級樓梯，那麼也只有一個方法，就是行一步上一級，所以s₁ = 1。如果他需上兩級樓梯，有兩個方法，就是一步上兩級，或者分兩步各上一級，s₂ = 2。 之後，我們也不難計算到s₃ = 3，s₄ = 5，s₅ = 8，s₆ = 13...

1, 1, 2, 3, 5, 8, 13... 聰明的你可能認得，這不就是大名鼎鼎的斐波那契數列（Fibonacci sequence）嗎？

斐波那契數列中，每個數字都是數列中前兩個數字的和，1 + 1 = 2，1 + 2 = 3，2 + 3 = 5，3 + 5 = 8，5 + 8 = 13... 為甚麼這個神奇的數列會出現在這樣的一條排列組合問題中呢？

試想想，假如小明要行上n級樓梯，他的最後一步有兩個可能性，行一級或兩級。假如最後一步是上一級，那麼他行上之前的手n - 1級有a_n-1個方法；假如最後一步是上兩級，那麼他行上之前的n - 2級有s_n-2個方法。因此行上n級樓梯有s_n-1 + s_n-2個方法，也就是說s_n = s_n-1 + s_n-2。這正正就是斐波那契數列生成的方法。

至於如何求s₁₀₀，也就是斐波那契數列中的第101項呢？我們當然可以慢慢加上攞去，不過這樣又麻煩又廢時，幸好我們有更聰明優雅的方法，就是利用公式：

至於這公式是如何得出呢？原來當有a_n + ba_n-1 + ca_n-2 = 0的關係時，a_n必定等如 C₁ λ₁ⁿ + C₂ λ₂ⁿ，其中λ₁與λ₂為λ² + bλ + c = 0的兩個根，而C1與C2為常數。

對斐波那契數列來說，a_n - a_n-1 - a_n-2 = 0。λ² - λ - 1 = 0的兩個根就是(1 + √5) /2及(1 - √5) /2。設a_n = C₁ [(1 + √5) /2]ⁿ + C₂ [(1 - √5) /2]ⁿ，代入a₁ = 1及a₂ = 1，就可以得到這公式。

最後，代入公式，得到573147844013817084101，也就是說小明有573147844013817084101種方法行上樓梯。

《魔雪奇緣2》：畫功依舊非凡，歌曲依然動聽

《魔雪奇緣》推出後平地一聲雷，反應好得令人難以置信，相信連迪士尼自己都意料不及。事隔五年，迪士尼再下一城，推出續集，新一集的質素如何呢？

史丹福覺得算是不過不失，有好有壞吧。先談談該讚的地方，迪士尼的畫功一流，相信這點是無容置疑的，上一集以雪為主題，把寒冬中各式各樣的冰雪形勢繪畫得出神入化，令人掘目相看。今集故事改為秋天漫天紅葉的景色，又是另一翻令人讚嘆的美麗。動畫的畫功依然非凡，不愧為動畫界的一哥。

上集《魔雪奇緣》爆紅的其中一個原因是一首極為洗腦的《Let it go》。今次的歌曲亦都精心設計，非常洗腦。新的主打《Into the unknown》到現時仍會偶爾在我腦袋中響起，洗腦程度相當驚人。其他的歌曲亦都非常悅耳，依舊動聽。

再加上姐妹情、探險的情節，《魔雪奇緣2》基本上就是複製上一集的成功公式。不過儘管如此，史丹福覺得這集仍然比上一集失色，為甚麼呢？

主要問題在於戲情上，電影中段的節奏過於緩慢，很大部分時間中戲情都沒有甚麼進展。可能歸根究底，是戲情沒有一個明確目標，亦營造不出一個危機感。以迪士尼近年的公主冒險電影作比較，《魔髮奇緣》中Rapunzel的目標是去see the light，《魔雪奇緣》Anna的目標是去找回姐姐避免王國被冰封，《魔海奇緣》 Moana的目標是把女神的心歸還。每套都有明確清晰的目標，而主角為了完成這些目標，又要經歷不同的危機。而《魔雪奇緣2》的問題在於劇情一直沒有交待主角的目標，我們就只知道要「救王國」，卻不知道如何救。事實上，我亦很難代入主角的危機，電影只靠神奇自然力量搗亂去營造危機感，但這些神奇自然力量其實也沒有做出甚麼危機來吧？

幸好去到中後段，大約自Elsa衝出怒海開始，電影漸漸開始回勇，令人感覺到危機感，目標也逐漸變得清晰，開始找回第一集的感覺。這部份之後，電影是非常出色的，無奈這只佔電影約四分之一的部分。

 總的來說，《魔雪奇緣2》嘗試重複首集的成功元素。畫功及音樂都做得非常出色，可惜劇情前部分節奏較為緩慢，幸好到中後段找回感覺，漸入佳境。其實電影是值得一看的，不過以迪士尼近期處於的超級高峰時期，之前都三套公主電影都非常出色（大家對《魔髮奇緣》及《魔海奇緣》可能較不熟悉，但這兩套都是極其精彩的作品，比起對《魔雪奇緣》，史丹福甚至更喜歡對《魔髮奇緣》），比較之下《魔雪奇緣2》難免有點相形見絀的感覺。

史丹福推介度：77/100