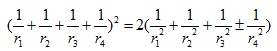極權政府為了欺壓人民,往往無所不用其極,從國家安全、國旗、國歌,到防疫、網絡版權、國民教育、洗頭艇,全都可以是極權政府的工具。但大家又有沒有想過連數學都可以被極權政府用來對付國民?
話說在上世紀70至80年代,前蘇聯最好的大學數學系位於莫斯科國立大學。整個莫斯科就只有這所大學的數學力學系提供純理論數學的課程。因此想投身數學研究的蘇聯學生都會以考進這所大學為目標。然而,蘇聯自史太林管治起已經對猶太人相當不友善,這位獨裁者在晚年更加變本加厲,把迫害猶太人變成國家的政策之一。雖然蘇聯未至於如納粹德國般屠殺猶太人,但在國家的政策下,猶太人仍然要受到種種不公平的對待。例如猶太學生幾乎是不可能考進莫斯科國立大學的。
莫斯科國立大學數學力學系頑固執行種族歧視政策,並有一套獨特的方法去篩走猶太學生,就是利用特別設計的數學入學試難題。這些數學題其本上並不是用來考核學生的能力,純粹是為了為難學生,有人就把這些題目稱為「棺材數學題」。但為了避免被人投訴,「棺材數學題」特意設計成看似很簡單,只用初等的數學語言就可以表達清楚,答案同樣也是看似很簡單,只用初等的數學技巧就可以解決。但這些問題其實非常巧妙,考生需要有極強的洞察力才可以解答得到。每當有人投訴考試不公平,考官就可以冠冕堂皇地把答案展示給投訴者,然後再嘲笑他們,「看,這題目多麼的簡單,是你學藝未精,連如此簡單的問題都解不到,我們學系才不收你啊!」這簡直是指鹿為馬。可惜的是,各式各樣的「指鹿為馬」到今天仍然經常在極權下出現。
更要命的是,這些題目是以口試形式來考學生的,也就是說考生不可以冷靜地慢慢思考,而是要即時給出答案,但「棺材數學題」是非常難以在短時間內想到的答案的。如果考生成功解答得到,考官又會即時轉另一條題目,不斷疲勞轟炸,直至考生答不到為止。
雖然「棺材數學題」的出現是沿於欺壓人民的極權,但單純從數學的角度來說,這些題目的確是很具學習價值的好題目。史丹福就在此分享幾題較簡單的「棺材數學題」,大家不妨試試。記得要先自己試算一下才看答案啊。如果直接看答案,你可能會誤以為它們是很簡單直接的題目,只有自己落手試試,才能領悟到其「棺材」之處。
- log23與log35,那個較大?(當然不可以用計算機)
- 給予兩條平行線段,在只用直尺的情況下把其中一條等分成六份。
- 在一圓形中,K是弦AB的中點。MN與ST是通過K的弦。MT與AB相交於P,NS與AB相交於Q。證明KP = KQ。
- 找出所有符合以下特性的函數F(x)
: R à R, ∀x1,
x2 ∈ R, F(x1) – F(x2) ≤ (x1
– x2)2
- 四個互相相切的圓形中,其中三個的圓心共線。第四個圓的半徑為r,其圓心與線的距離為x。以r表達x。
大家落手試了問題嗎?解答得到嗎?
以下是答案:

- 設兩條平行線段分別是l1與l2,其中l1比l2長。設l1的頂點為A與B,l2的頂點為C與D。我們先證明我們可以把l2等分成兩分。連接AC與BD,令它們的延線相交於E。連接AD與BC,設它們相交於F。連接EF,使EF的延線與AB相交於G。G就是AB的中點。我們可能繼續用同樣的方法,把AB線段等分成四份,再等分成八份。
如下圖所示,使AC與A6D的延線相交於H。把H與A1至A5相連,這5條線就可以把l2等分成六份。
3. 這是大名鼎鼎的幾何定理--蝴蝶定理(Butterfly
theorem)。如果考生對歐氏幾何有深入認識,並早已學習過這定理的證明,那自然會解答得到。否則要獨立地自己想出證法,應該是非常困難的。
∠NSK
=
∠TMK
∠SKN
=
∠MKT
ΔNSK ~ ΔTMK
KS/SN = KM/MT
設E
與F
分別為SN
與MT
的中點。
KS/SE = KM/MF
∠ESK
=
∠FMK
ΔESK ~ ΔFMK
∠SEK
=
∠MFK
設O
是圓的圓心。
∠OKQ
+
∠OEQ
= 90
o + 90
o = 180
o,因此OKQE
共圓。同樣地,∠OKP +
∠OFP = 90
o
+ 90
o = 180
o,因此OKPF
共圓。
∠KOQ
=
∠SEK =
∠MFK =
∠KOP
OP = OQ
ΔOPQ
是等腰三角形,OK
是垂線。根據等腰三角形的性質,KP
= KQ
。
4.
F(x)
必為一常數函數。5. 大家覺得這個四圓構圖是否有點熟口熟面呢?史丹福曾經在舊文章《日本寺廟幾何學》中介紹過笛卡兒在1643年提出的笛卡兒定理(Descartes'
Theorem)。該定理指出對於四個互相交接於一點,而四個圓形的半徑分別是r1、r2、r3與r4,那麼
幕府時期的日本人也獨立於西方自己研究出這定理,他們更利用這定理解開了不少寺廟幾何學題目。我們也不妨利用一下這定理去計算這「棺材數學題」。
設C1的半徑為1,C2與C3的半徑分別為a與1-a,C4的半徑是r。
經過一點運算之後應可得到a (1 - a) = r / (1 + r) 。
接著我們考慮ΔO2O3O4。三角形的面積是(O2O3) x/2 = [a
+ (1 – a)] x/2 = x/2。但我們同時可以用海龍公式(Heron’s formula)去求面積。O2O3 = 1,O2O4 = a + r,O3O4 = 1 - a + r。
大家看完答案後就會明白,「棺材數學題」其實並不牽涉太高深的數學。除了笛卡兒定理,其他問題使用的定理與技巧都只是標準高中程度的數學。大家甚至可能會誤以為問題浪得虛名,不見得太難,但其實這正是題目的厲害之處。這樣大學就可以名正言順地貶低猶太學生的數學能力,理直氣壯地不收他們。
猶太裔數學家弗倫克爾(Edward
Frenkel)是加州大學柏克萊分校數學系教授。他是位表示論、代數幾何與數學物理學的專家,數學功力絕對不容小覷。不過他不幸地生於前蘇聯,小時候就曾經受到這些「棺材數學題」的摧殘,結果不能考上莫斯科國立大學,只可以在次一等的學校中攻讀數學。他後來在訪問中表示,這些「棺材數學題」最可怕的地方不在阻止學生升上心儀大學,而是在於撤底地摧毀學生的自信心。大學入學試令弗倫克爾大受打擊,他更一度以為自己的數學知識真的次人一等,不配進行高等的數學學術研究。他寧願大學直接地告訴他,大學不收取他是因為他的猶太血統。那麼他至少可以知道自己考不進莫斯科國立大學只是制度的不公,與自己的能力無關。幸好弗倫克爾之後重拾信心,並且頑強對作出抵抗。他偷入莫斯科國立大學旁聽,並在地下學術刊物中發表自己的研究。結果得到了美國哈佛大學賞識,邀請他赴美深造,最後獲得了哈佛大學的博士學位,並成一位出色的數學家。
「棺材數學題」與弗倫克爾的故事告訴我們,在面對極權的壓迫時不要放棄,只要繼續相信自己,繼續做對的事,終有一天可以戰勝不公,贏得公義。