法國著名軍事與政治家,曾經帶領法國軍隊橫掃歐洲的拿破崙(Napoleon
Bonaparte)似乎與數學是風馬牛不相及,但事實上拿破崙是位數學高手。不少大名鼎鼎的法國數學家,如拉普拉斯(Pierre-Simon Laplace)及傅利葉(Joseph Fourier)都與他私交甚篤。
拿破崙甚至是法蘭西科學院數學部的院士。他自己非常熱愛學習數學及科學知識,他的身邊總是聚集著一大批科學家和學者,即使在作戰時拿破崙都要帶著學者與他同行,並與他們一起討論數學及科學問題。
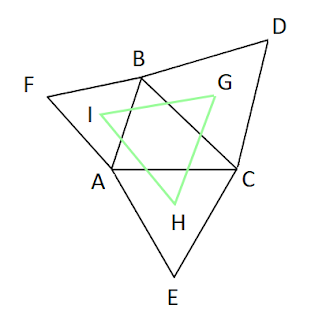
甚至有一條數學定理是以拿破崙來命名的,「拿破崙定理」指出以任意三角形各邊為邊分別向外側作正三角形,再把三個三角形的中心連線,就會構成一個正三角形。
證明如下:
畫出ΔABF與ΔACE的外接圓,設它們相交A與O兩點。
∠AOB=180°-∠AFB(opposite ∠s, cyclic quadrilateral)=180°-60°=120°
同樣地,∠AOC=120°
∠BOC=360°-∠AOB-∠AOC (∠s at a point)=360°-120°-120°=120°
∠BOC+∠BDC=120°+60°=180°
所以BDCO是一個圓內接四邊形。
我們再畫出ΔBCD的外接圓。設L、M及N分別是AO與HI、BO與IG及CO與GH的交點。
BO是以I為中心的圓及以G為中心的圓的公弦(common chord),所以BO與IG互相垂直(perpendicular)。類似地,AO與HI及CO與GH也是互相垂直。
考慮四邊形IMOL,∠LIM=360°-∠IMO-∠ILO-∠LOM=360°-90°-90°-120°=60°
同樣地,∠MGN及∠NHL都是60°,所以ΔGHI是等邊三角形。
雖然也有人質疑這定理未必是由拿破崙提出,這定理的歷史也很難考究了,但拿破崙熱愛數學,他真的研究出這條定理也不足為奇啊。
除了數學之外,拿破崙也都很欣賞與支持其他學科的科學家。他曾邀請意大利物理學家伏特(Alessandro
Volta)到巴黎展示電學實驗,當他知道伏特經濟有困難時,更立即出錢資助。英國化學家戴維(Humphry Davy)用電解方法發現新元素鉀與鈉,拿破崙不管當時英法交戰,特別頒發勳章給他。英國醫學家詹納(Edward Jenner)發明了預防天花的牛痘疫苗,當英國報紙還在討論種牛痘會不會「令人生牛角」時,拿破崙已經率先號召全體法國人接種,並讚許詹納是位偉人。
拿破崙的科學成就雖然說不上很高,但他尊重科學家的精神,令人敬重,也非常值得大家學習。他的尊重孕育了法國的數理風氣,是科學種子在法蘭西土地盛放的原因之一。在今天的香港,學校把STEM掛在嘴邊,政府又時常強調要發展創科,但社會的主旋律似乎都依然是「口講科學,心中想錢/利益」,這樣科學只會淪為口號,永遠不會有真正的發展。也許,我們的社會需要更多真心喜歡與尊重科學的人。